Определение
Часто ли противоречия встречаются в нашей повседневной жизни? Что такое противоречие? Каковы причины его возникновения? Давайте постараемся дать понятию “противоречие” определение.
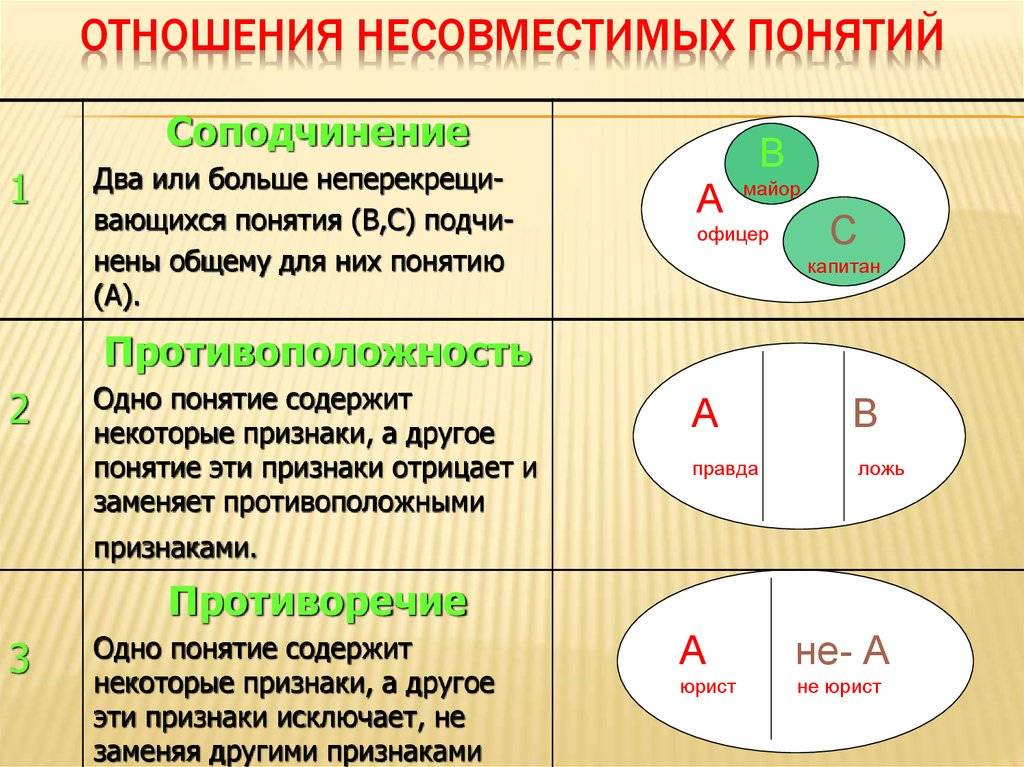
Этот термин достаточно широк для интерпретаций и применяется в различных сферах жизни, но его значение остается неизменным, константой в любом контексте. В классическом понимании, противоречие состоит из логической несовместимости между двумя или более суждениями.
Это происходит, когда предложения, рассматриваемые вместе, дают два вывода, которые образуют логические, обычно противоположные по смыслу версии.
Иллюстрируя общую тенденцию в прикладной логике, закон несогласия Аристотеля гласит: «Невозможно, чтобы одно и то же было и не было присуще одному и тому же в одно и то же время в одном и том же отношении».

Современные противоречия
В современном мире предостаточно основных и неосновных противоречий. Первые носят глобальный характер и напрямую связаны с дальнейшей судьбой человечества. К таким конфликтам можно отнести разные взгляды на стратегию глобализации, несоответствие потребления человечеством ресурсов и их реальное наличие, спор между наукой и религией, споры о капитализме и характере труда. Рано или поздно человечеству придется прийти к единой точке зрения, учитывая интересы всех групп, банально для продолжения нормальной жизнедеятельности. Обращаясь к Аристотелю, было бы логично упомянуть его квадрат противоречия, являющийся формальным ответом на вопрос, что такое противоречие. Логический квадрат или квадрат несогласия является диаграммой, представляющей отношения между четырьмя основными категориальными положениями. Аристотель не составлял диаграмму собственноручно, но появление ее можно все же отнести к более ранней деятельности философа. Данная теория о противоречиях несколько столетий спустя была оформлена в схему Апулеем и Боэтием. В традиционной логике предложение является устным суждением, а не смыслом утверждения, как в современной философии языка и логики. Категориальное положение – это простое предложение, содержащее два члена, субъект и предикат, в которых предикат либо утверждается, либо отрицается субъектом.

Логика Аристотеля
Каждое категорическое предложение может быть сведено к одной из четырех логических форм.
- Так называемое «A» предложение, универсальное утверждение, форма которого на латыни является omne S est P, обычно переводится как «каждый S является P».
- Предложение «Е», универсальное отрицание, латинская форма nullum S est P, обычно переводимое как «S не является P».
- Предложение «Z», конкретное утверждение, латинское quoddam S est P, обычно переводится как «некоторые S – это P».
- Предложение «О», конкретное отрицание, латинский quoddam S non est P, обычно переводится как «некоторые S не являются P».
Аристотель утверждает, что между этими четырьмя видами суждения существуют определенные логические связи. Он говорит, что каждому утверждению соответствует ровно одно отрицание и что каждое утверждение и его отрицание «противоположны», так что всегда один из них двух тезисов должен быть истинным, а другой ложным. Примерами противоречий являются «каждый человек белый» и «не каждый человек белый» (также читается как «некоторые люди не белые»), «ни один человек не белый», а «какой-то человек белый».
В то время, как греческий философ Аристотель не представляет конкретного отрицательного, поскольку «некоторые A не являются Б», но поскольку «не каждый A есть Б», неизвестный автор прокомментировал его труд под названием Peri Hermaneias ответным тезисом , буквально значившим «определенное А не является В». Далее во всех средневековых работах, затрагивающих тему логики, было принято представлять конкретное суждение именно таким, менее радикальным образом, чем Аристотель. Но это не доказывает его неправоту.
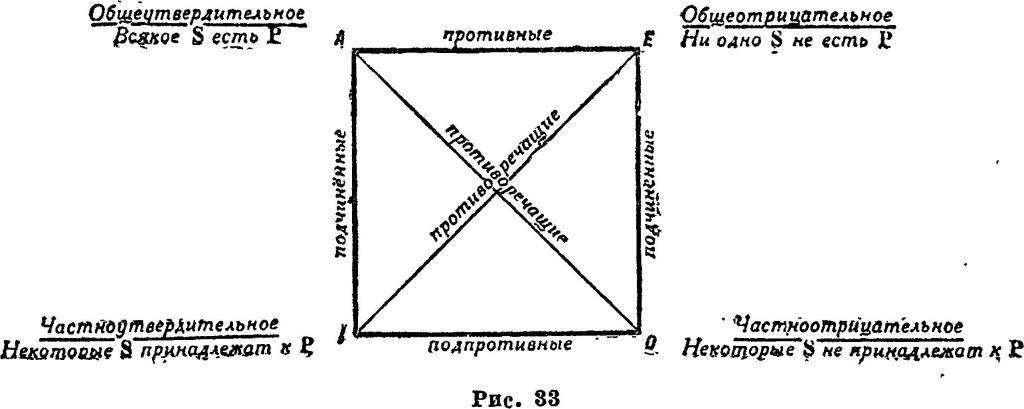
Эти положения стали основой диаграммы, созданной Боэцием и используемой средневековыми логиками для классификации логических отношений. Предложения помещаются в четыре угла квадрата, а отношения представлены в виде линий, нарисованных между ними, из чего последовательно получается «Логический квадрат».
Практическая работа №9«Изучаем графический редактор Paint» (задания 4 – 7)
Задание 4
1. Запустите графический редактор Paint ().
2. Откройте файл Клоуны (Мои документы\ 6класс\ Заготовки).
3. Раскрасьте черно – белого клоуна так, как раскрашен разноцветный клоун. Рекомендуемая последовательность действий:1) активизируйте инструмент Выбор цвета;
2) щелкните на объекте, цвет которого следует скопировать;
3) с помощью инструмента Заливка закрасьте нужную область.
4. Сохраните результат работы под тем же именем, но в собственной папке.
Задание 5
1. Откройте файл Флаги (Мои документы\ 6класс\ Заготовки).

2. Каждый из трех горизонтальных прямоугольников заполните цветом, красная, зеленая и синяя составляющие которого имеют указанные числовые значения.
Вспомним как это выполняется:
1. Запустите графический редактор Paint и выполните команду .
2. В открывшемся диалоговом окне Изменение палитры щелкните на кнопке Определить цвет; обратите внимание на информацию в правой нижней части экрана. 3. Задайте значения в полях ввода для основных цветов и проследите за изменениями в окне Цвет\3аливка.
3. Задайте значения в полях ввода для основных цветов и проследите за изменениями в окне Цвет\3аливка.
4. Установите, какие цвета получатся при заданных значениях основных цветов.
3. Подумайте, сколько разных трехцветных флагов можно составить, используя данные цвета. Размножьте заготовку флага и изобразите все придуманные вами варианты.
4. Сохраните результат работы под тем же именем, но в собственной папке.
Задание 6
1. Откройте файл Лепестки (Мои документы\ 6класс\ Заготовки).
2. Цвет контура четырех центральных лепестов замените на синий. Используйте возможности “цветного ластика”.
Для этого:1) с помощью инструмента Выбор цета сделайте цвет контура основным;
2) сделайте синий цвет фоновым;
3) выберите инструмент Ластик;
4) нажмите правую кнопку мыши и, не отпуская её, пройдите ластиком линии рисунка, цвет которых следует заменить.
3. Сделайте цвет контура четырёх боковых лепестков зеленым.
4. Сохраните результат работы под тем же именем, но в собственной папке.
5. Завершите работу с графическим редактором.
Задание 7
1. Запустите графический редактор.
2. Используя все известные вам инструменты, нарисуйте черным контуром на белом фоне забавную физиономию.
3. Сделайте несколько копий полученного рисунка.
4. Внесите изменения в отдельные детали рисунка, так чтобы каждая физиономия имела свое выражение. Для этого выделяйте нужные фрагменты (инструмент Выделение) и применяйте команды
Отразить/повернуть и Растянуть/наклонить меню Рисунок. Мелкие изменения можно вносить, закрашивая отдельные пиксели после увеличения рисунка (инструмент Масштаб).
5. Раскрасьте все рисунки и сохраните их в собственной папке под именем Шутка.
6. Завершите работу с графическим редактором.
Теперь мы умеем
создавать сложные объекты из фрагментов;
копировать цвет заданной области;
получать цвет по кодам составляющих его цветов;
изменять цвет части существующей линии.
Несогласия в политике
Частота возникновения противоречий в политике достаточно высока, потому что эта сфера очень подвижна, а также поводы для препирательств возникают часто. Противоречия могут возникать между политическими партиями с различными друг от друга идеологиями, между государством и гражданами. Такие противоборства являются основой политико-властных отношений и постепенно интегрируются во все сферы нашей жизни. Существует два фундаментальных метода разрешения подобных спорных ситуаций: первый заключается в тотальном подавлении и, буквально, уничтожении противника. Суть второго метода состоит в поиске консенсуса путем переговоров, диалога. Естественно, второй метод куда демократичнее и применяется чаще первого, но не стоит отрицать, что первая методика тоже часто встречается на политической арене.